SURE formulas

Setup

Model:

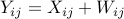
$Y_{ij} = X_{ij} + W_{ij}$

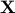is 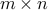real or complex valued
noise 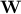is iid Gaussian with mean 0 and variance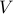

Estimator:

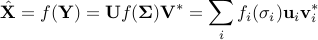
$hat{mathbf{X}} = f(mathbf{Y}) = mathbf{U} f(mathbf{Sigma}) mathbf{V}^* = sum_{i} f_i(sigma_i) mathbf{u}_i mathbf{v}_i^*$

where 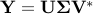$mathbf{Y} = mathbf{U} mathbf{Sigma} mathbf{V}^*$ is any SVD

General SURE formulas

Definition:

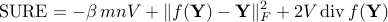
$mathrm{SURE} = -beta , mnV + |f(mathbf{Y}) - mathbf{Y}|_F^2 + 2V , mathrm{div}, f(mathbf{Y})$

in real case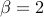
in complex case

Real case

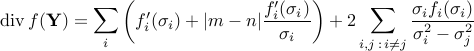
$mathrm{div}, f(mathbf{Y}) = sum_{i} left( f'_i(sigma_i) + |m-n|frac{f'_i(sigma_i)}{sigma_i}right) + 2sum_{i, j , : , i neq j} frac{sigma_i f_i(sigma_i)}{sigma_i^2 - sigma_j^2}$

Complex case

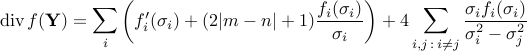
$mathrm{div}, f(mathbf{Y}) = sum_{i} left(f_i'(sigma_i) + (2|m-n|+1)frac{f_i(sigma_i)}{sigma_i}right) + 4sum_{i, j , : , i neq j} frac{sigma_i f_i(sigma_i)}{sigma_i^2 - sigma_j^2}$

Special case: Singular Value Thresholding (SVT)

Definition:

$hat{mathbf{X}} = mathrm{SVT}(mathbf{Y}) = sum_{i} (sigma_i - lambda)_+ mathbf{u}_i mathbf{v}_i^*$

SURE formula:

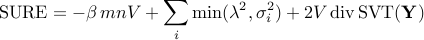
$mathrm{SURE} = -beta , mnV + sum_{i} min(lambda^2, sigma_i^2) + 2V , mathrm{div}, mathrm{SVT}(mathbf{Y})$

in real case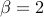
in complex case

Real case

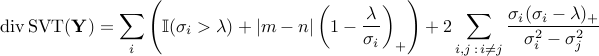
$mathrm{div}, mathrm{SVT}(mathbf{Y}) = sum_{i} left(mathbb{I}(sigma_i > lambda) + |m-n|left(1 - frac{lambda}{sigma_i}right)_+right) + 2sum_{i, j , : , i neq j} frac{sigma_i (sigma_i - lambda)_+}{sigma_i^2 - sigma_j^2}$

Complex case

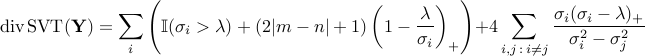
$mathrm{div}, mathrm{SVT}(mathbf{Y}) = sum_{i} left(mathbb{I}(sigma_i > lambda) + (2|m-n|+1) left(1 - frac{lambda}{sigma_i}right)_+ right) + 4 sum_{i, j , : , i neq j} frac{sigma_i (sigma_i - lambda)_+}{sigma_i^2 - sigma_j^2}$

Block SVT

Definition:

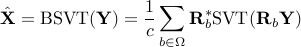
$hat{mathbf{X}} = mathrm{BSVT}(mathbf{Y}) = frac{1}{c}sum_{binOmega} mathbf{R}_b^* mathrm{SVT}(mathbf{R}_b mathbf{Y})$

where

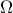is a collection of subsets of rows of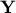
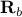$mathbf{R}_b$ is the restriction to the rows indicated by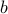
is a positive scalar

SURE formula:

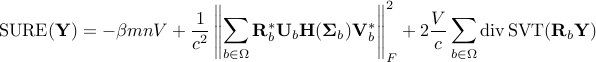
$mathrm{SURE}(mathbf{Y}) = -beta{mn}V + frac{1}{c^2}left|sum_{binOmega} mathbf{R}_{b}^{*}mathbf{U}_{b}mathbf{H}(mathbf{Sigma}_{b})mathbf{V}_{b}^{*}right|_F^2 + 2frac{V}{c} sum_{bin{Omega}} mathrm{div}, mathrm{SVT}(mathbf{R}_{b}mathbf{Y})$

where

$mathbf{R}_b mathbf{Y} = mathbf{U}_bmathbf{Sigma}_b mathbf{V}_b^*$ is any SVD
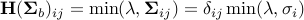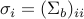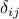$mathbf{H}(mathbf{Sigma}_{b})_{ij} = min(lambda,mathbf{Sigma}_{ij}) = delta_{ij} min(lambda,sigma_{i})$ with $sigma_{i} = (Sigma_{b})_{ii}$ ( $delta_{ij}$ is Kronecker's delta)
in real case
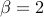in complex case

Divergence formula for all matrix arguments

(See the hypothesis in Theorem 4.6 for this formula to hold)

Definition:

$mathrm{div}, (f(mathbf{X})) = sum_{i:, s_i > 0} left[a_if'(s_i) + b_ifrac{f(s_i)}{s_i}right] + sum_{i:, s_i = 0} c_i f'(0)+ 2betasum_{ineq j,, i, j} d_i d_jfrac{s_i f(s_i)}{s_i^2 - s_j^2}$

where

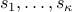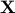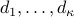$s_1,ldots, s_{kappa}$ are the distinct singular values of , and $d_1,ldots, d_{kappa}$ their multiplicities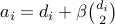
$a_i = d_i + beta{d_i choose 2}$
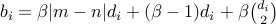
$b_i = beta|m-n|d_i + (beta - 1)d_i + beta{d_ichoose 2}$
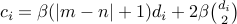
$c_i = beta(|m - n|+1)d_i + 2beta{d_ichoose 2}$
in real case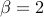
in complex case