introduction
Singular Value Thresholding (SVT) is an algorithm to minimize the nuclear norm of a matrix, subject to certain types of constraints. It has been successfully used in many matrix-completion problems (for more on the matrix completion problem, see Exact matrix completion via convex optimization by E.J. Candès and B. Recht). The SVT algorithm is described in the paper A singular value thresholding algorithm for matrix completion by J-F. Cai, E.J. Candès and Z. Shen.
The version of SVT available at this website is restricted to equality constraints of the form:

However, the user can easily modify it to handle inequality constraints of the form:

SVT can also work with more general constraints (e.g. any Lipschitz-continuous convex function), but for simplicity, this is not implemented in the code below.
The SVT algorithm solves the following problem:

where the first norm is the nuclear norm (the sum of singular values) and the second norm is the Frobenius norm. Problem (P3), for large values of tau, is closely related to problem (P2):

Problem (P2) is often used as a proxy for problem (P1), since (P1) is not convex:
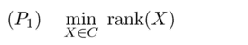
Please see links to the right for access to code and papers on matrix completion.